Riduzione dei manici

Questo progetto è stato parzialmente finanziato dall’ANR TheoGar.
Il contenuto e le immagini sono tratti da questo testo di Patrick Dehornoy.
Traduzione di Ester Dalvit.

Che cos’è la riduzione dei manici?

La riduzione dei manici è un metodo, o meglio un algoritmo, di manipolazione delle trecce, che consente di risolvere il problema della banalità di una treccia, cioè di poter dire se i suoi fili sono veramente intrecciati.
Questo metodo non è l’unico conosciuto, però è forse il più veloce: anche applicandolo a diagrammi con migliaia di incroci, permette di giungere alla risposta in un tempo molto breve (anche meno di un secondo).
Per spiegarlo più chiaramente abbiamo bisogno di parlare di trecce, diagrammi, parole, manici...

Che cos’è una treccia?

Una treccia è una collezione di curve, che chiameremo fili, nello spazio tridimensionale; essa descrive una treccia “fisica”, come ad esempio una treccia dei capelli. Una treccia può essere composta da un qualsiasi numero di fili, che sono fissati alle estremità e possono “intrecciarsi” nello spazio tra i due supporti. I fili devono inoltre “scorrere” sempre da un‘estremità all‘altra, senza tornare indietro.

Come si può rappresentare una treccia?

Il modo più comune di rappresentare una treccia consiste nel disegnare un diagramma, cioè una figura costituita da alcune linee (che rappresentano i fili della treccia) che si possono incrociare, come ad esempio in questa immagine.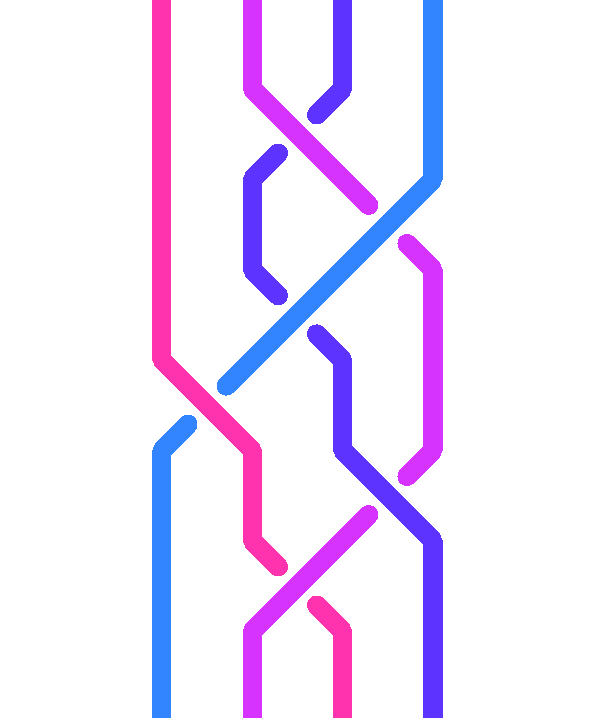

Più precisamente si parla di diagramma a n fili. Quello dell’immagine ha 4 fili.
Un diagramma può essere visto come la proiezione piana di una treccia; esso deve rispettare tre regole:

i fili sono “in discesa”, ossia vanno sempre dall’alto verso il basso: non sono ammesse inversioni a U!
gli incroci sono posti su altezze diverse
ad ogni incrocio, uno dei due fili viene spezzato, per indicare che esso passa dietro all’altro nella treccia tridimensionale.

Come si può descrivere un diagramma?

Si possono usare delle parole, cioè sequenze finite di lettere ‘a’, ‘A’, ‘b’, ‘B’, ecc. Se “leggiamo” un diagramma dall’alto verso il basso, vediamo una successione di incroci. Per descriverlo, basta specificare questi incroci in ordine, cioè dire quali fili si incrociano ad ogni livello e quale dei due fili passa sopra all’altro.
Di solito si numerano le posizioni da 1 a n in un diagramma a n fili e si chiama a (oppure σ₁) l’incrocio in cui il filo in posizione 2 passa sopra a quello in posizione 1; b (oppure σ₂) sarà l’incrocio in cui il filo in posizione 3 passa sopra a quello in posizione 2, e così via.
In modo simmetrico, si usa A (oppure σ₁^-1) per l’incrocio in cui il filo in posizione 1 passa sopra a quello in posizione 1, B (oppure σ₂^-1) per l’incrocio in cui il filo in posizione 2 passa sopra a quello in posizione 3, e così via.

a → σ₁ →

, A → σ₁^-1 →

b → σ₂ →

, B → σ₂^-1 →

Per esempio, il diagramma dell’immagine precedente si può descrivere con la parola BcbACb (oppure σ₂^-1 σ₃ σ₂ σ₁^-1 σ₃^-1 σ₂).
Viceversa, data una parola, si può disegnare il diagramma corrispondente. Ecco allora che diagrammi e parole contengono esattamente le stesse informazioni.

Quando si può dire che due trecce sono “uguali”?

Due trecce sono “uguali”, o meglio isotope, se possono venir deformate una nell’altra in modo continuo. In altre parole, se si può passare da una treccia all’altra muovendo i fili, ma mantenendo sempre gli estremi fissati e non permettendo ai fili di passare uno attraverso l’altro. I diagrammi di due trecce isotope sono detti equivalenti.
Ad esempio, i due diagrammi seguenti mostrano la proiezione di trecce isotope e un movimento che porta una nell’altra.

Che cos’è il problema di isotopia delle trecce?

Il problema di isotopia delle trecce consiste nel decidere, date due trecce, se esse sono isotope o meno.
Si dice che due parole sono equivalenti se si può passare da una all’altra con una sequenza finita delle seguenti mosse:

introdurre o cancellare due lettere adiacenti che siano una l’inversa dell’altra: ad esempio si può passare da cABbab a cAab e viceversa;
scambiare due lettere adiacenti se nell’ordine alfabetico non sono vicine: ad esempio si può passare da cABbab a AcBbab e viceversa;
se s è una lettera e r è la lettera che la precede in ordine alfabetico, sostituire srs con rsr o viceversa: ad esempio si può passare da cABbab a cABaba e viceversa.

Si può mostrare che due parole sono equivalenti se e solo se i corrispondenti diagrammi sono isotopi. Allora il problema di isotopia può essere espresso in un altro modo: date due parole, decidere se esse sono equivalenti.

È difficile risolvere il problema di isotopia delle trecce?

Non è né facilissimo né estremamente difficile. La prima soluzione è stata trovata dal matematico Emil Artin negli anni ’30. Oggi si conoscono almeno una dozzina di soluzioni diverse, che partono da approcci diversi. Tutte però si basano su risultati matematici abbastanza sofisticati. Uno di questi metodi è la riduzione dei manici, che è descritta in queste pagine.

Che cos’è il problema di banalità delle trecce?

Si dice che un diagramma è banale se è isotopo a un diagramma senza incroci. Il problema della banalità di una treccia consiste nel decidere se un dato diagramma è banale.
Il diagramma senza incroci viene scritto come la parola vuota, cioè la parola senza lettere! Allora il problema di banalità si può riformulare nel modo seguente: data una parola, decidere se essa è equivalente alla parola vuota.

I problemi di isotopia e di banalità sono collegati?

Sì, essi sono due problemi equivalenti. Il problema di banalità è un caso speciale del problema di isotopia, in cui una delle due trecce è banale (o una delle due parole è vuota). Allora, se si risolve il secondo problema, automaticamente si trova anche una soluzione del primo.
Viceversa, dati due diagrammi D e D' a n fili, essi sono isotopi se e solo se il diagramma, ottenuto incollando D sopra l’immagine di D' attraverso uno specchio orizzontale, è banale. In questo modo, una soluzione del problema di banalità è anche una soluzione del problema di isotopia.

Che cos’è un manico?

Un manico è una parola con alcune caratteristiche speciali.
Se con s indichiamo una qualsiasi lettera minuscola (per esempio a, b, ecc.) e con S la sua maiuscola (A, B, ecc.), chiamiamo s-manico una parola del tipo s...S, dove tutte le lettere intermedie (se ce ne sono) precedono s nell’ordine alfabetico.
Allo stesso modo chiamiamo S-manico una parola del tipo S...s, dove tutte le lettere intermedie (se ce ne sono) precedono s nell’ordine alfabetico.
Per esempio, la parola cbAC è un c-manico.
Diciamo che una parola contiene un manico se una sua sottoparola è un manico (di uno qualsiasi dei due tipi).
Un manico si può vedere anche sul suo diagramma: il primo e ultimo incrocio si trovano nella stessa posizione orizzontale e hanno orientazioni opposte, mentre tutti gli incroci intermedi, se ce ne sono, sono più a sinistra.
Per esempio, la parola BcbACb contiene il c-manico cbAC e il diagramma corrispondente, con il manico evidenziato in nero, è il seguente:

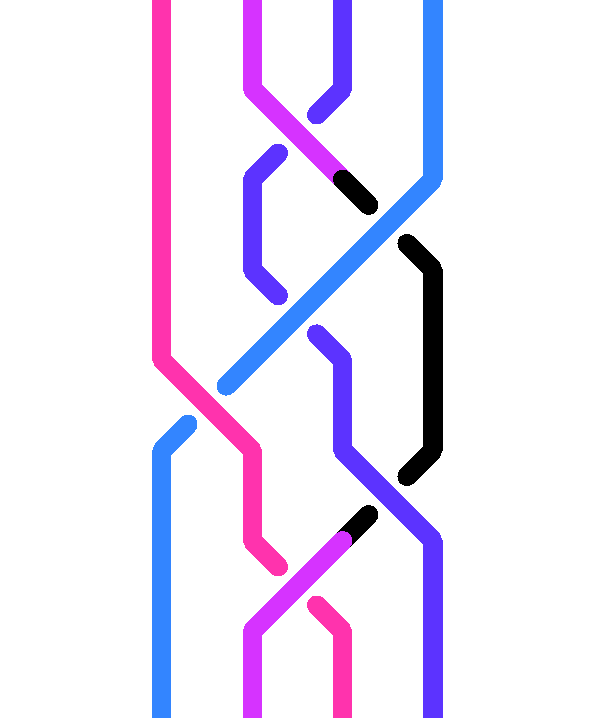
Una parola può contenere più di un manico: per esempio ABcbACbAab contiene il c-manico cbAC e l’A-manico Aa.
Se una parola contiene almeno un manico, chiamiamo primo manico quello più a sinistra.

Cosa significa ridurre un manico?

L’obbiettivo dell’algoritmo di riduzione dei manici è quello di cercare di eliminare tutti i manici. Il passo base consiste nel trasformare un manico in una parola equivalente che chiamiamo ridotta.
Sia h un s-manico e sia r la lettera che sta subito prima di s in ordine alfabetico. La ridotta di h è la parola ottenuta da h nel seguente modo:

cancellare la s iniziale e la S finale
sostituire ogni r in h (se ce ne sono) con Rsr e ogni R in h (se ce ne sono) con RSr.

Allo stesso modo, se h un S-manico, la ridotta di h è la parola ottenuta da h nel seguente modo:

cancellare la S iniziale e la s finale
sostituire ogni r in h (se ce ne sono) con rsR e ogni R in h (se ce ne sono) con rSR.

Per esempio, la ridotta del c-manico cbAC è BcbA e la ridotta dell’A-manico Aa è la parola vuota.

Sul diagramma questo procedimento corrisponde a spingere il manico verso sinistra, in modo che il filo che forma il manico passi al di là degli incroci che si trovano immediatamente alla sua sinistra.
La figura seguente mostra la treccia ottenuta da quella dell’immagine precedente dopo aver ridotto il manico.

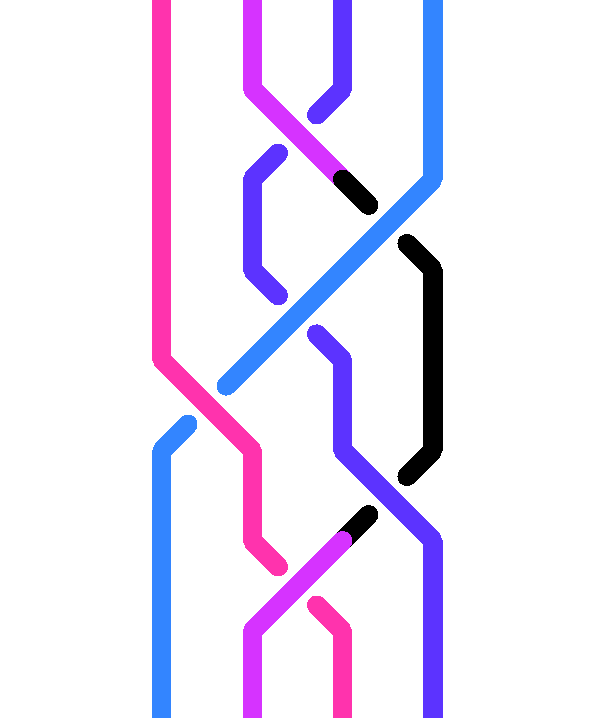
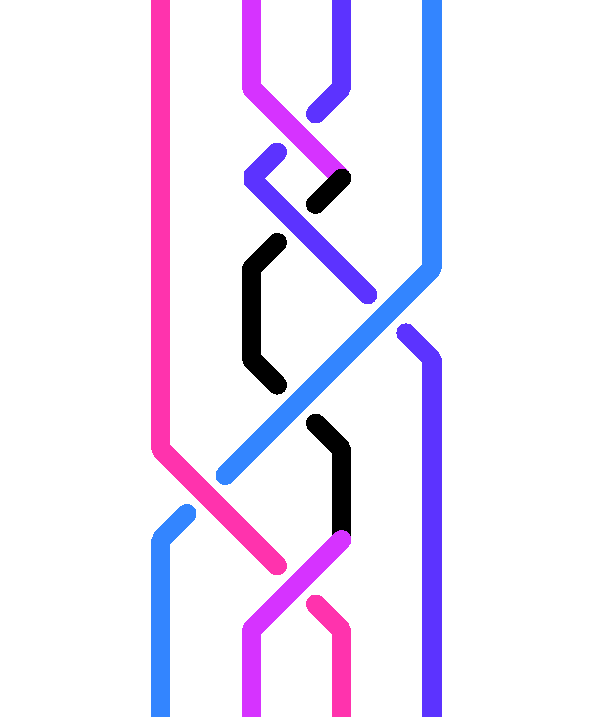
Si può notare che la riduzione dei manici è un’equivalenza, cioè i due diagrammi associati sono isotopi. Si vede anche che dopo la riduzione di un manico, effettivamente esso non c’è più, ma il procedimento può creare nuovi manici alla sinistra di quello che abbiamo ridotto.

Come funziona l’algoritmo di riduzione dei manici?

Si parte da una parola w e si riduce il primo manico, cioè lo si sostituisce con la sua ridotta. Si rifà lo stesso procedimento con la nuova parola ottenuta, e si continua finché non ci sono più manici da ridurre. Si può dimostrare che a questo punto:

se otteniamo la parola vuota, allora la parola iniziale w è equivalente alla parola vuota;
se otteniamo una parola non vuota, allora la parola iniziale w non è equivalente alla parola vuota.

Quindi la riduzione dei manici risolve il problema della banalità.

L’applet presente in questa pagina può aiutare a visualizzare l’algoritmo.

Perché questo algoritmo funziona?

A questa domanda è difficile rispondere! A priori, non c’è nessun motivo per cui l’algoritmo debba terminare: potremmo continuare a ridurre manici e crearne di nuovi all’infinito! Potrebbe anche succedere che una parola, nonostante non contenga manici, sia equivalente alla parola vuota.
Ma si può dimostrare che questo non succede mai, e anzi l’algoritmo converge sempre e risolve il problema della banalità. Questo risultato è abbastanza difficile e richiede metodi matematici sofisticati. La ragione principale per cui l’algoritmo funziona è l’esistenza di un certo ordine delle trecce. Per saperne di più si può leggere

P.Dehornoy, I.Dynnikov, D.Rolfsen, B.Wiest, Why are braids orderable?, Panoramas et Synthèses vol. 14, Soc. Math. France (2002).
C.Kassel & V.Turaev, Braid groups, Springer (2007).