A journey through the mathematical theory of braids

Under construction! Comments welcome.
Ask your questions writing me an email. If I find your questions interesting, I will publish them here with answers.

Clic on a question to see the answer on scroll down the page.

General questions

Is there more to say about braids besides what is in the movie?

Of course, a lot! Some examples:

‘Braids acts on curves in the punctured disc’, that means that if you put a closed string around the braid strands and pull it to the other side of the braid, you generally get a different curve, which is almost unpredictable, unless... you formalize curves similarly to wath is done to braids in Chapter 1, you understand how each elementary braid modifies each elementary curve, and you make some computations! Look at this video and this one to get an idea.
There have been some attempts to use braids in cryptography, in the spirit of Chapter 2. You can read a nice explanation in French by Patrick Dehornoy.
The imagination of mathematician also led them to consider more general braids, which describe different braiding phenomena: for example ‘welded’ braids describe some of the braiding of tubes in 4-dimensional space!
Mathematicians also consider braids with endpoints on surfaces different from a disc (recall the definition in Chapter 1, 1:28), for example a sphere or a torus (an empty doughnut)...
And who knows how many new interpretations and uses of braids are to be discovered!

It does not seem these topics have something to do with the school curriculum. Moreover, much of the stuff is too difficult. Why do you propose school activities on braids?

I have a lot of answers.

The formalization of braids is not too difficult for high school students and is a nice example to train in formalization and pass from empirical to abstract. The typical problem would be to describe a braid talking at the phone (first step) or using a text message with the least number of characters (second step). Also checking the group properties and commutativity is not difficult and can be used to recall those concepts.
Some of the difficult stuff can be told in an informal and fascinating way, so it can serve as motivation and to give an idea of mathematics beyond school. Many students think that mathematics is calculations and that there is nothing to discover in mathematics. Themes like the one in the movie can change students' impressions.
Many themes that are in the curriculum are touched by the video: equivalence relations, associative and commutative properties, inverses, symbolic description and computations, permutations. Proposing them to students can be a way to verify how confident they are with these ideas and if they can recognize the same structure and properties in different contexts. Which is one of the main aims of teaching school mathematics.
I think it is useful to make the students do mathematics, at least sometimes, and not only listen to the teacher explaining and solve exercises. The problem of braid description is a wonderful example: it starts from concrete objects and is not too difficult.
Some activity can be proposed even to primary school children: describe braids (just in the form: "take three strings. Pass the leftmost over the central one. Now pass the rightmost under the central one. Etc") find an inverse for a braid (using ribbons like in the dance of chapter 4). These activities enhance observation skills and abstract thinking and prepare the students for the next steps.
Since the topics are not closely related to school curricola, they can be proposed even to weak students, who will not have the disadvantage of poor competences. They will participate in the activity at the same level of the other students and this will help their motivation.
I have actually done such activities with students and their response was very positive. They were fascinated and motivated.

Disclaimer: Of course I do not think that the teaching goals can be achieved only with this topic or active learning methodologies. But I think there are possibilities that are still not fully exploited in schools and the movie and the workshops are a proposal to make more experimentations.

Chapter 1

Why is braid isotopy (chapter 1, 3:11) an equivalence relation?

Braid isotopy is:

reflexive: a braid can be deformed to itself... with no deformation at all!
symmetric: if a braid can be deformed into another, viewing the deformation backwards we can turn the second braid into the first one;
transitive: if a braid can be deformed into another and the latter into a third one, we can view the two deformations as a single one and thus turn the first braid into the third one.

I could turn a braid in space upside down or bring its back to the front. This does not change the braid! Right?

No! Although these movements do not change your physical object but only rotate it, we want to keep track of the direction in which the strands ‘flow‘ and the order in which they start.

This is more natural if you think of a braid made combing the hair: its ends are attached to the head and the braid ‘flows‘ downwards.

What is the solution of the question at chapter 1, 4:58?

Have a look at 7:47 to 8:00.

Why do the strands have different colors?

There is an artistic reason: colors help distinguish the strands and give more pleasant images.

But the main reason is that colors give a straightforward way to find the permutation associated with the braid: if you fix an order of colors on the left (say, RYBG: red, yellow, blue, green, from the bottom strand to the top one), then the order of colors on the right side gives the permutation associated to the braid.

For example, the left braid in the picture has RYBG on the left and YBRG on the right, while the right braid has RYBG on the left and BRYG on the right.

If you replace letters by numbers, you get one of the common ways to denote a permutation: for the first braid

1 2 3 4
2 3 1 4

and for the second

1 2 3 4
3 1 2 4

Note that if you want to compare two braids, it is not enough to compare the order of the colors on just one side of both braids! Rather we have to compare how the color are mixed going from one side to the other. For example, the two braids in chapter 1, 9:12 are equal, as is shown there, even if the colors of the strands do not match.

Using colors to emphasize permutations is also used in chapter 2, 4:10, to define pure braids.

Why do strands change color when you compose two braids? I find it confusing.

Colors help recognize the permutation associated to a braid: it gives a way to recognize each strand. By convention I chose an order for the strand colors on the left side, namely red, yellow, blue, green starting from the bottom.

Composition means stacking braids, so if the first braid has a nontrivial permutation, then the colors at the end of the first braid will not match with those at the beginning of the second braid.

In the resulting braid I want each strand to have its own color, following the convention. So the strands of the second braid which is composed have to change colors (unless the permutation associated to the first braid is the identity).

How can I get the permutation associated to a braid?

One way is the following: assign a number to each strand end on the left, starting from the bottom strand. Copy the same numbers to the right, putting each number in the position of the corresponding strand. As an example, consider the braid in the picture.

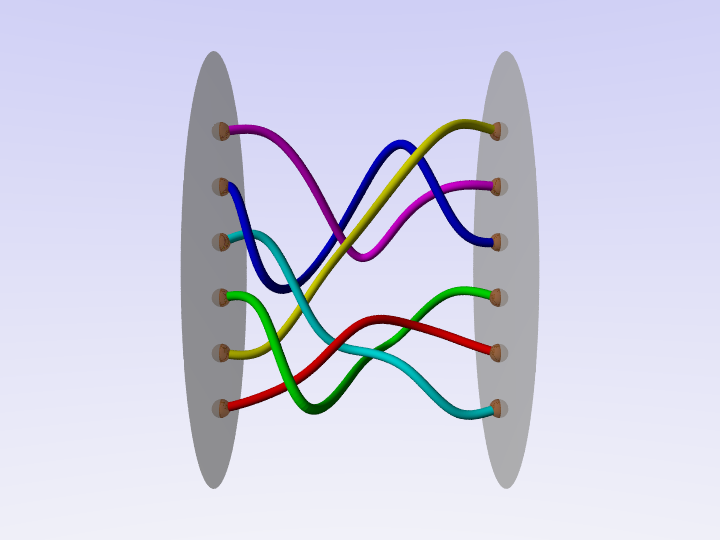
The associated permutation will be

1 2 3 4 5 6
4 1 3 5 6 2

Another way is to describe permutation by cycles. In this case, assign a number to each vertical strand position, starting from the bottom strand. Then follow the ‘braid flow’ and write the 2-cycle (a,a+1) whenever the strand in position a crosses the strand in position a+1. In the example above it would start with

the cyan strand crossing the blue one, they are in positions 4 and 5 so write (4,5);
then the yellow one crossing the green one, they are in positions 2 and 3 so write (2,3);
then again the blue and cyan strands crossing, they are in positions 4 and 5 so write (4,5);
then the red and green ones, they are in positions 1 and 2 so write (1,2). Here note that even though the green strand had the number 3 in the beginning, its position has changed after the crossing with the yellow one;
and so on.

Thus the permutation in this case will start with (4,5)(2,3)(4,5)(1,2)... and it can be simplified to (2,3)(1,2)...

Here is another way to distinguish two braids: compose each braid with itself until you get the identity permutation for the first time. Count how many times you repeated the braids: if the two numbers are different, then the braids are different. Correct?

Yes! To prove it, you have to check that:

repeating any braid you will get the identity permutation and
the number you defined is an invariant of braids.

Why did you choose the positive real numbers (chapter 1, 6:29) to make a comparison between braid composition and a numerical operation?

I wanted to use product and not sum because I write braid composition in a multiplicative way; for example, I denote the trivial braid by 1 and the inverse of a braid A by A^-1.
The set of real numbers is not a group under multiplication since 0 has no inverse. So I could choose real non-zero numbers but I thought just positive numbers would be easier.

Alternatively, I could choose integer numbers with the operation of product. Then the neutral element would be 0, the inverse of A would be -A and summing A and B would be A+B. Associativity reads (A+B)+C = A+(B+C) and commutativity A+B = B+A. This is completely analogous but does not mimic the way I write braid composition as close as multiplication of real numbers does.

Is the braid with all strands parallel (chapter 1, 8:10) really a braid?

Is 0 really a number? Even if it stands for ‘nothing’? Even if n+0=n for any n?

Is 1 really a number? Even if n·1=n for any n?

Yes! And I would say that the braid with all strands parallel is the most important one because it permits to define inverses.

Seen from an empirical viewpoint, in the definition of braids we fix the endpoints and draw strands to connect them. Nothing prevents us to draw unbraided strands!

Why do you check the inverse of a braid on both sides? Is one not sufficient? (chapter 1, 8:47)

Because composition is not commutative, so it is not obvious that a left inverse is also a right inverse.

You first present some properties of composition (associativity and commutativity) and only then check that composition give the structure of a group. Wouldn't it be more logical to switch the order?

Everyone has their favorite way to introduce and explain concepts. My choice comes from the fact that almost everybody recalls from primary school that ‘the sum and the product are associative and commutative’ while almost nobody has a clear mental image of neutral element and inverses (maybe they seem too obvious concepts?). I want to connect what I am explaining to what people usually know already. This is the reason for my choice.

Why do you consider mainly braids with four strands?

Because 4 is the least number of strands for which the braids are general: the group of braids with 4 strands has both kinds of relations (the braid relation and the commutativity of crossings involving distinct pairs of strands).

In fact, braids with two strands form a group which is isomorphic to the group of integers (each braid is characterized by the number of crossings counted with sign: see next question) and braids with three strands have no crossings involving distinct pairs of strands.

If I propose an activity in the school, asking students to find a language to describe braids (find the generators) I would start from braids with two strands. Is it a good idea?

Wonderful! You can ask to find a very short way to describe a two-strands braid. In fact, you only need an integer number, counting how many times the left strand passes in front of the right one. If the left strand passes behind the right one, you will use negative numbers. And if It passes once in front and once behind, you can simplify... And what braid will have the number 0?

Said in another way, there is an isomorphism between the group of braids with two strands (where the operation is composition) and integers (where the operation is the sum).

However, this is not a general example about braids: here the composition is commutative, while in braid groups with more strands it is not.

Why did you choose the σ_i notation described in 9:58?

The main reason is that this is the standard notation used by mathematicians. Using a letter with a number as a subscript is very practical: you can describe braids with any number of strands, because you only need to use natural numbers.

Also the notation for inverses is very clear: you can simplify σ₁^-1σ₁ σ₂ σ₂^-1 σ₁^-1 to get σ₁^-1.

Another possibility would have been to use A instead of σ₁, a instead of σ₁^-1, B instead of σ₂, b instead of σ₂^-1, and so on. In this way, the word baAbBBb could be simplified to b. But we could not describe braids with more than 27 strands since there are 26 latin letters!

However, both are multiplicative notations: composition is written as juxtaposition and the neutral element (the trivial braid) is denoted 1.

A different way is given by additive notation! For example, use 0 for the neutral element, +1 instead of σ₁, -1 instead of σ₁^-1, +2 instead of σ₂, -2 instead of σ₂^-1, and so on. In this way, a word of the form +2-1+1-2+2 could be simplified to +2. Note that we keep even + signs! Only 0 is allowed to carry no sign. And we simplify whenever we find a pair of subsequent signed symbols of the form +n-n or -n+n.

Another reason for my choice of multiplicative notation is that with the additive one we would be tempted to forget + signs and to sum the numbers in a word, both of which are not allowed in our context.

Chapter 2

Why do you say we could look for a sequence all our life long and do not find an answer?

We do not know whether a sequence exists, and if it exists how long it is. Sure we could sistematically try all the possible sequences of moves, starting from the shortest ones and increasing the length. But if we find none, at which point should we stop? How can we know whether the sequence we were looking for was just a bit longer than the ones we tried?
In other words, the sistematic procedure may give an answer “Yes, a sequence exists” or give no answer at all.

In the graph you draw two lines to visualize complexity. What do you mean?

I will answer as soon as possible.

I am scared by Artin's statement to try the algorithm on a living person!

This is just a joke! It means it is not feasible to use such an algorithm in practice, because it would require a very long time to end.

Chapter 3

Why can't we study knots just in the same way as braids, defining an operation and a group structure and all that?

It would be wonderful if we could! But we have not yet found a suitable operation which plays the role of braid composition.
To be honest, there is a meaningful operation, called connected sum, which allows to join two knots in a similar way as braids are composed. The problem with it is that knots can not be inverted that is, given a knot A, there is no knot B such that the connected sum of A and B produce the trivial knot, a knot with no crossings! In other words, the set of knots with this operation is not a group.

Chapter 4

You show a Bavarian dance in the beginning. There is a pole in the middle, does it make any difference in the description of braids?

I will answer as soon as possible.

Why should plat closure be interesting? Is the other closure not enough?

I will answer as soon as possible.

A journey through the mathematical theory of braids

General questions

Questions on Chapter 1

Questions on Chapter 2

Questions on Chapter 3

Questions on Chapter 4

General questions

Chapter 1

Chapter 2

Chapter 3

Chapter 4