A journey through the mathematical theory of braids
The movie is divided into four chapters, each of about 15 minutes. Here is a short summary of the contents.
The first contains the basic concepts: the formalization of braids and the group structure on the set of braids. Artin presentation of the braid group is given. A braid is now described by a word on a set of letters, the generators.
The second chapter deals with the word problem: when do two words represent the same braid? Two algorithms are presented to solve this problem, the Artin braid combing and the handle reduction.
In the third chapter knots are presented and put in relation with braids. In the final part the Jones polynomial is introduced: it is a powerful knot invariant that was defined via braids.
The last chapter describes braids as dances, that is, motions of points in the disc. The Hilden group, a subgroup of the braid group, is defined and related to another way of closing braids.
Here you can find some stills from the movie and a summary of each chapter. More informations cane be found in the FAQ page.
Braids are everywhere in common life! Jewellery, hairdressing and many decorative objects use braided patterns.
Braids are studied also as mathematical objects, because their mathematical structure is very rich and deep.

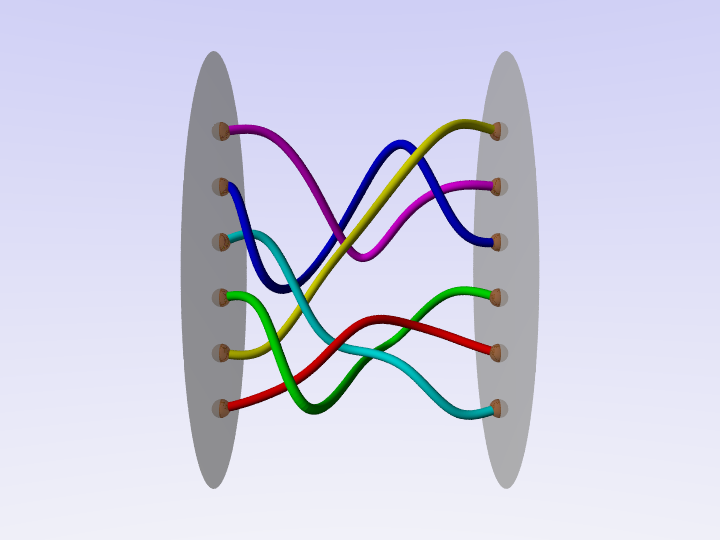
A first definition of a braid is a collection of strands between two parallel discs.
Braids are considered the same if they can be deformed into each other without cutting the strands and keeping the endpoints fixed (braid isotopy).
Two braids can be joined to obtain a new one. This operation is called composition and gives a group structure to the set of braids with a fixed number of strands.
The elementary braids are those having just one crossing. Any braid can be viewed as a composition of elementary braids and thus it can be described by a word.
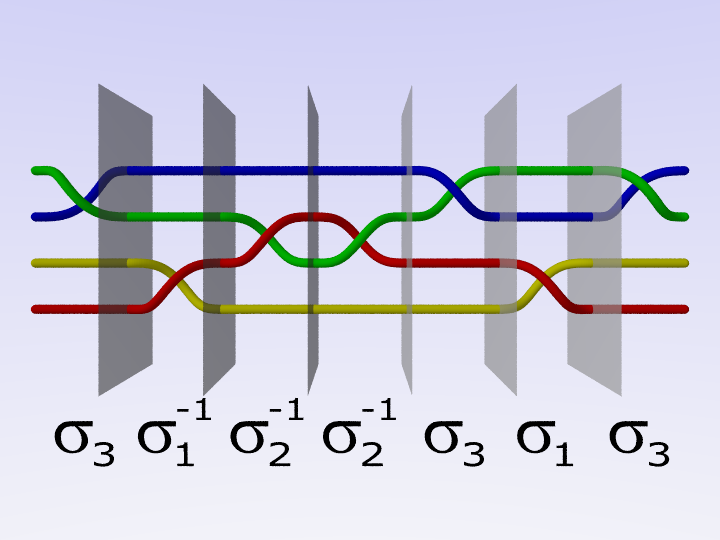

The group of braids can be described by means of the Artin presentation. The generators are the elementary braids. The relations are of two kinds: one is typical of the braids groups and the other is a commutative relation between distant crossings.
To describe a braid we can use a word in the generators, but two different words may represent the same braid.
The problem of deciding whether two words represent the same group element is called word problem.
To solve it one needs an algorithm, that is a procedure to follow to obtain an answer in a finite number of steps.

In arbitrary groups the word problem is not solvable, that is, there is no algorithm to solve it.
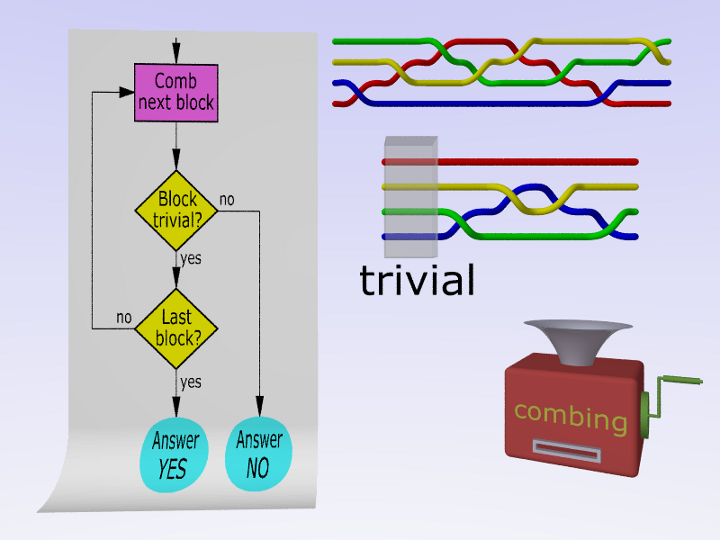
However, the word problem in braid groups is solvable. The first algorithm was proposed by Artin in the 1930s and is called braid combing.
Still, its complexity is exponential in the size of the braid words, that makes it infeasible to use combing in practice.
Various other algorithms are known to solve the word problem in braid groups. The fastest (so far) is Dehornoy's handle reduction algorithm. The first paper describing it has been published in 1997.
Like braids, also knots, closed strings, are very common objects in everyday life and they are also of great interest to mathematicians!
Similarly to braids, two knots are considered the same if they can be deformed into each other without cutting the strings.
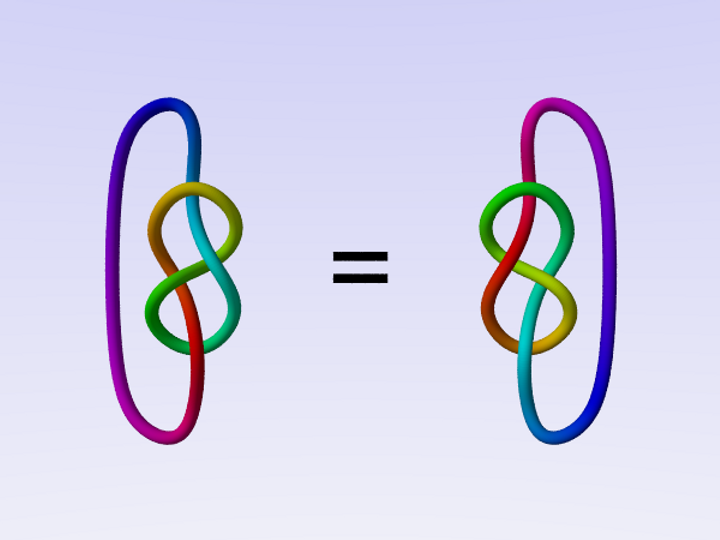
Some knots, such as the figure eight knot, are the same as their mirror image (mathematicians say that they are achiral), while others, such as the trefoil knot, are not.
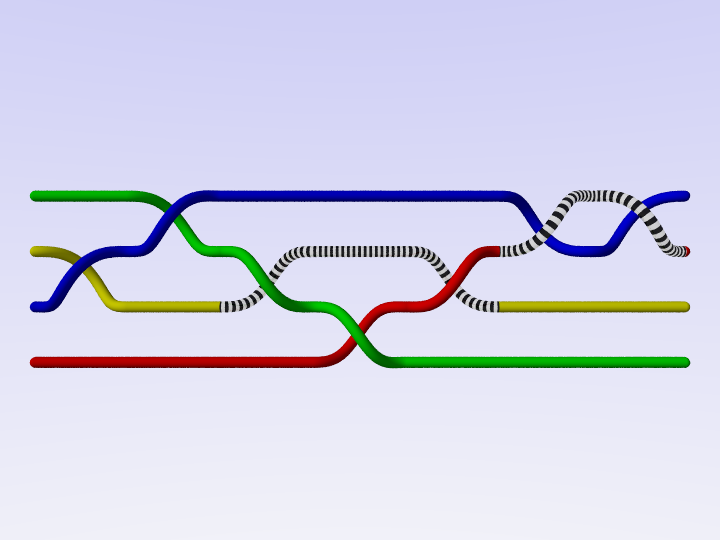
To obtain a knot from a braid, we just need to tie the strand ends together.
Vice versa, it is possible to obtain every knot as the closure of a braid. The first proof is due to Alexander: in the 1930s he proposed an algorithm to put a knot into the form of a closed braid.
When do two closed braids give the same knot?
To answer, we introduce the operations of conjugation and stabilization. These two moves are enough to characterise the braids giving the same knot, as Markov theorem ensures. Unfortunately, this theorem is not constructive.

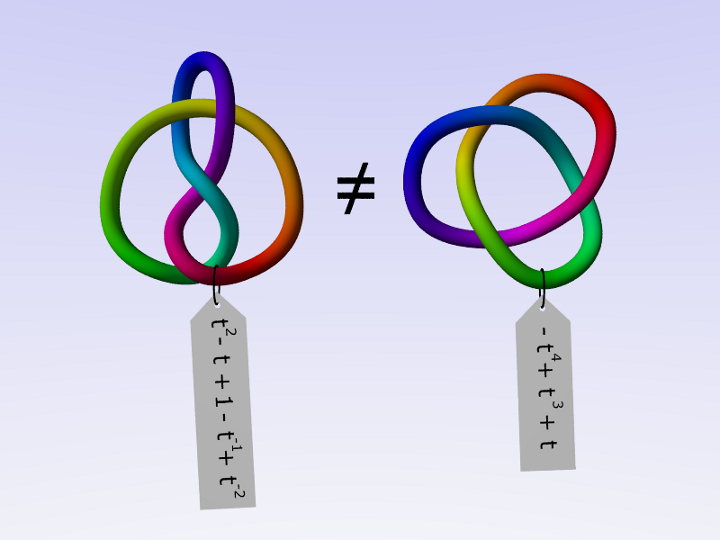
A way to distinguish knots is to define invariants, that is, to associate to each knot an object in some mathematical structure such that equivalent knots are associated to the same object.
Vice versa, if two knots are associated to different objects, then they are surely different.
One of the most powerful invariants is the Jones polynomial, that was first defined in 1984 via braids and their closure.
Its discovery opened new insights into knot theory, and was so crucial that Jones was awarded the Fields Medal for it.

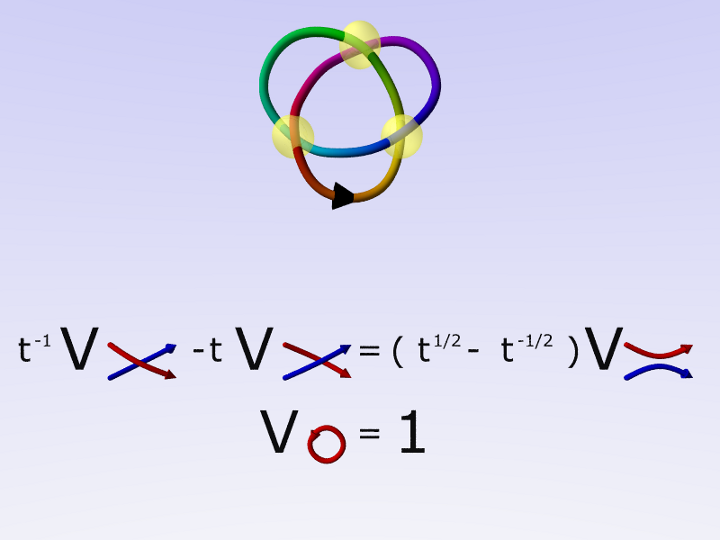
There are a couple of ways to compute the Jones polynomial, that do not need to pass through braids. One of them consists of using the skein relations to simplify knots.
A tradition in many countries of German culture is the maypole dance. Similar dances are performed also in South America.
Dancers move around a pole holding ribbons and entwined them in various ways.

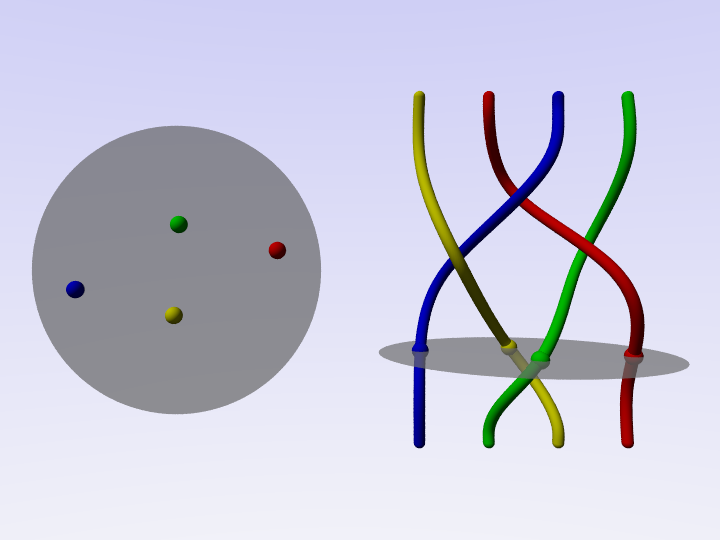
Dances can be formalised as motion of points in the disc. Keeping track of the movements we can obtain a braid.
Vice versa, given a braid, we can transform it into a dance.
We can consider specific dances, where dancers are in pairs and hold hands. Their formalization yields a subgroup of the braid group with an even number of strands, called Hilden group.
A set of generators consists in three kinds of braids, where the strands are paired.

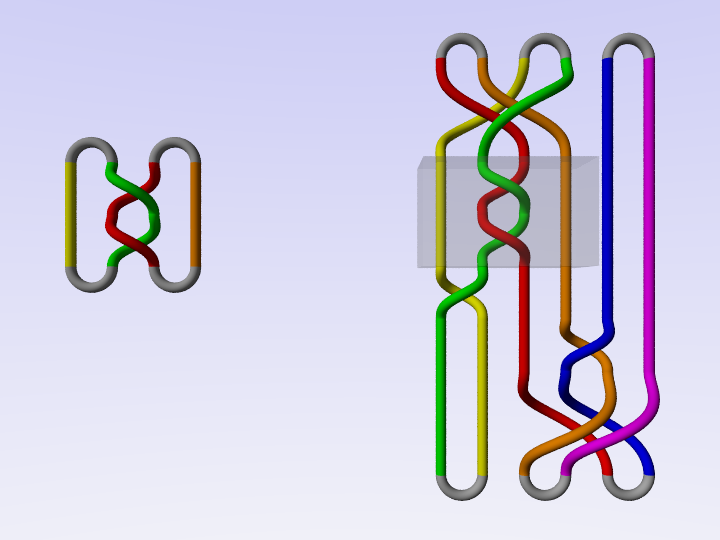
Another way to obtain a knot from a braid is to use the plat closure.
Similarly to what happens with the Alexander closure, every knot can be obtained via plat closure of a braid.
A theorem of Birman (1970s) characterises the braids giving the same knot via plat closure. In other words, it is analogous to the Markov theorem but refers to the plat closure.
One of the permitted moves is composition with Hilden elements.


Finally we present the membership problem: is it possible to decide whether a given braid belongs to the Hilden subgroup or not?
A solution is contained in a 2009 preprint. We do not report it but just note that again we found an algorithmic problem.
Some references
- Emil Artin, Theory of braids, Ann. of Math. 48, 1947.
- Patrick Dehornoy, A fast method for comparing braids, Adv. Math. 125, 1997.
- Colin C. Adams, The knot book: an elementary introduction to the mathematical theory of knots, 1994.
- Joan S. Birman, Braids, links, and mapping class groups, 1974.
- Stephen Tawn, A presentation for Hilden's subgroup of the braid group, Math. Res. Lett. 15, 2008.
