Un viaggio nella teoria matematica delle trecce

Capitolo 1 - Il gruppo treccia

Dappertutto si possono trovare delle trecce: nelle pettinature, nelle cinture di pelle, nei gioielli... molti oggetti di uso comune sono decorati con le trecce.

Le trecce vengono studiate anche come oggetti matematici e danno vita a dei risultati molto variegati e profondi.

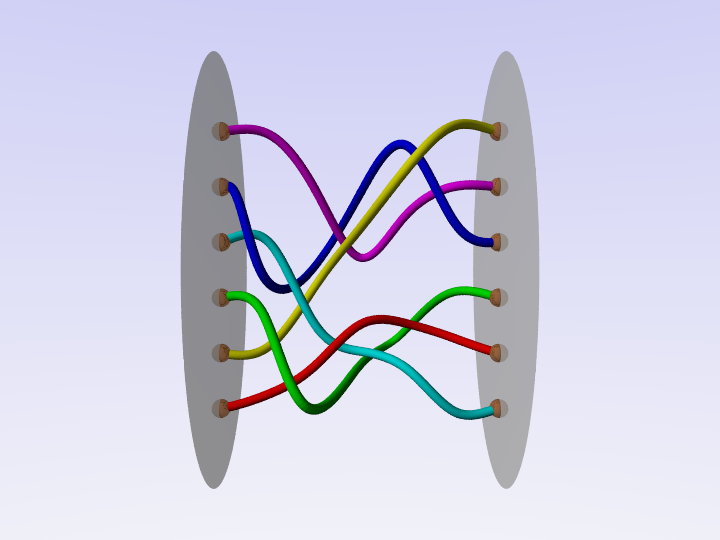
Una treccia può essere definita come una collezione di fili che collegano dei punti fissati su due dischi.

Si considerano uguali le trecce che possono essere deformate una nell'altra mantenendo gli estremi fissati sui dischi e senza tagliare i fili.

Due trecce con lo stesso numero di fili possono essere incollate una dopo l'altra: questa operazione si chiama composizione e dà una struttura di gruppo all'insieme delle trecce.

Le trecce elementari sono quelle che hanno un solo incrocio. Ogni treccia può essere vista come composizione di trecce elementari e venire quindi descritta da una parola, una sequenza di simboli, ognuno dei quali rappresenta una treccia elementare.

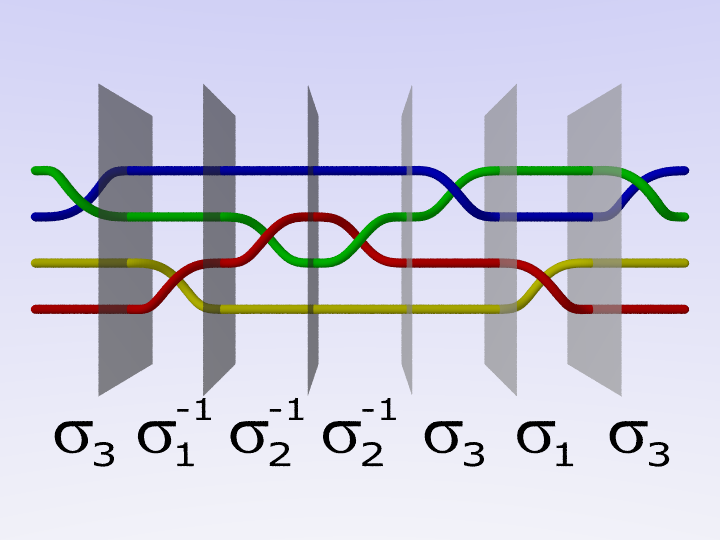
Il gruppo delle trecce con un numero fissato di fili può essere descritto tramite la presentazione di Artin. I generatori sono le trecce elementari. Le relazioni sono di due tipi: una è tipica dei gruppi treccia, mentre l'altra permette di scambiare fra loro incroci “distanti”.

Capitolo 2 - Il problema della parola

Per descrivere una treccia possiamo usare una parola, le cui lettere sono i generatori, ma due parole diverse possono rappresentare la stessa treccia.

Il problema della parola in un gruppo consiste nel dare una procedura effettiva, un algoritmo, per stabilire se due parole qualsiasi descrivono o meno lo stesso elemento nel gruppo.

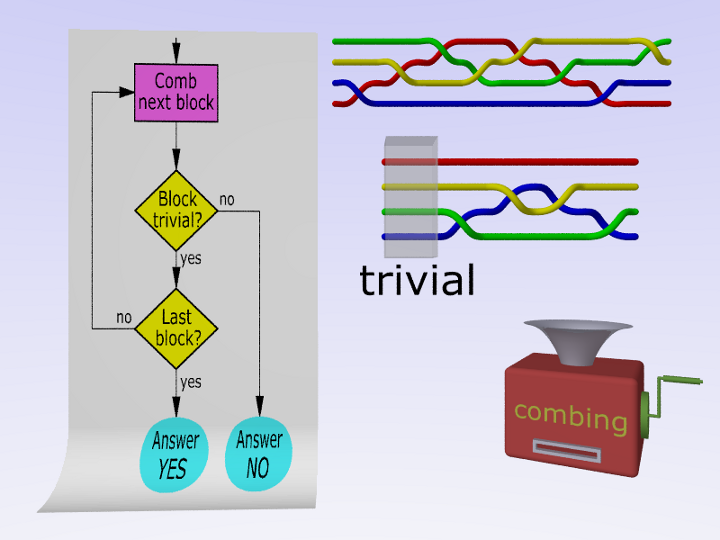
In generale, per gruppi qualunque, il problema della parola non si può risolvere, cioè non ci sono algoritmi per rispondere.

Invece nei gruppi treccia si può: il primo algoritmo venne proposto da Artin negli anni '30 del secolo scorso e consiste nel “pettinare” le trecce, mettendole in una forma particolare.

La complessità dell'algoritmo è però esponenziale nella lunghezza della parola; questo lo rende assolutamente inutilizzabile!

Per fortuna sono stati proposti vari algoritmi più efficienti. Il migliore (finora) è il metodo di “riduzione dei manici” proposto da Dehornoy in un articolo del 1997.

Capitolo 3 - Nel mondo dei nodi

Anche i nodi sono oggetti molto comuni e vengono formalizzati dai matematici, che li considerano cordicelle le cui estremità sono legate tra loro.

Analogamente a quanto accade per le trecce, due nodi vengono considerati uguali se si può trasformare uno nell'altro senza tagliare le cordicelle.

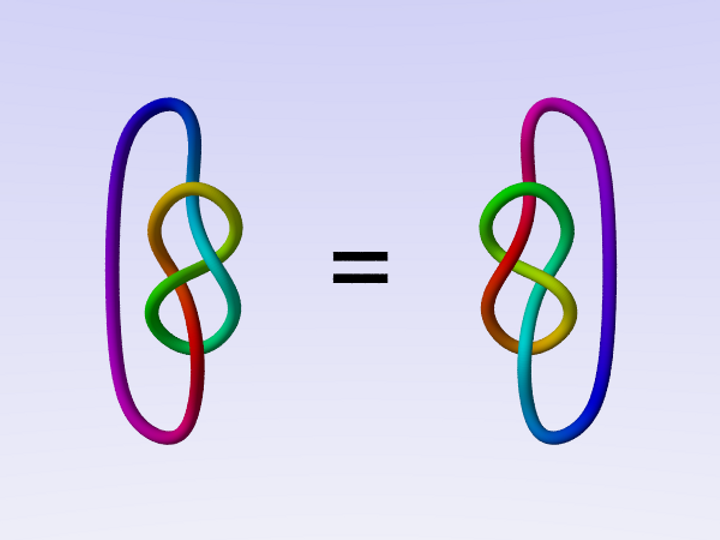
Alcuni nodi, come il nodo a otto, sono uguali alla loro immagine speculare, mentre altri, come il trifoglio, non lo sono.

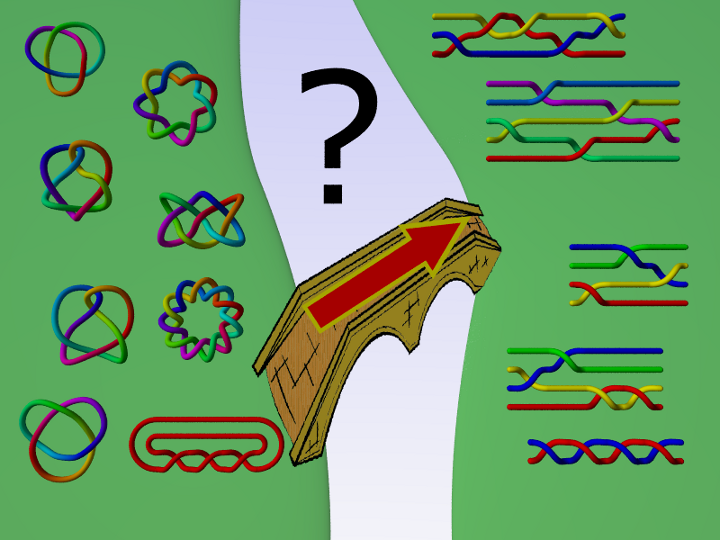
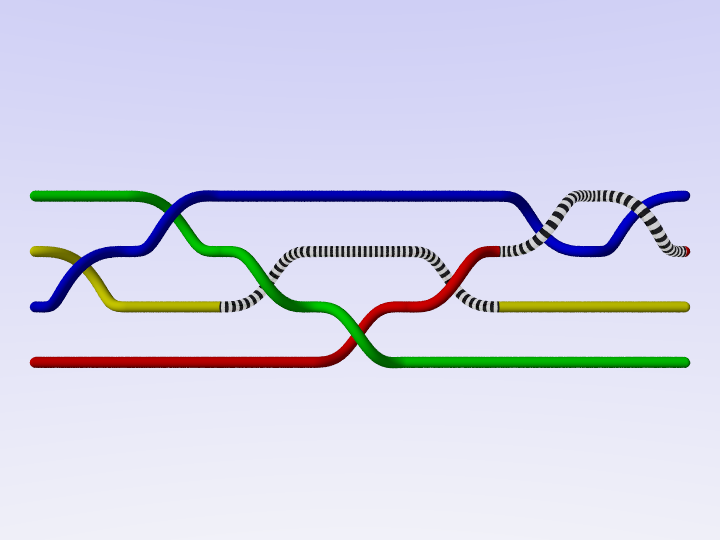
Per ottenere un nodo a partire da una treccia basta collegare tra loro le estremità dei fili.

Viceversa, ogni nodo può essere costruito come chiusura di una treccia. La prima dimostrazione di questo teorema è di Alexander, che propose un algoritmo per fare ciò negli anni '30 del secolo scorso.

Quando due trecce, se vengono chiuse, danno lo stesso nodo?

Per rispondere introduciamo due mosse, la coniugazione e la stabilizzazione. Il teorema di Markov assicura che due trecce danno lo stesso nodo se e solo se sono legate da una sequenza di mosse di questo tipo. Ma non è facile capire se una tale sequenza esiste o no!

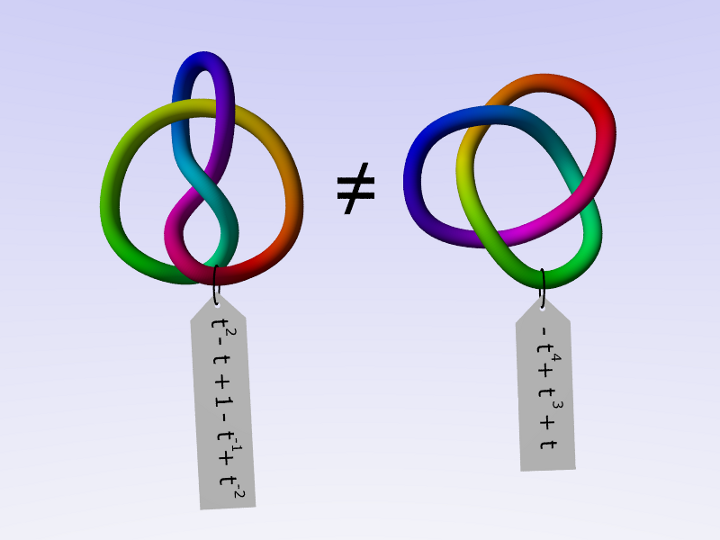
Un modo per distinguere nodi diversi consiste nell'usare degli invarianti, cioè associare a ogni nodo un oggetto matematico in modo che nodi uguali corrispondano allo stesso oggetto.

Viceversa, se due nodi sono associati a oggetti diversi, allora sicuramente non sono lo stesso nodo.

Uno degli invarianti più potenti per i nodi è il polinomio di Jones, definito nel 1984 attraverso le trecce e la loro chiusura.

La sua scoperta diede nuovo impulso alla teoria dei nodi e la rivoluzionò al punto che Jones vinse la medaglia Fields.

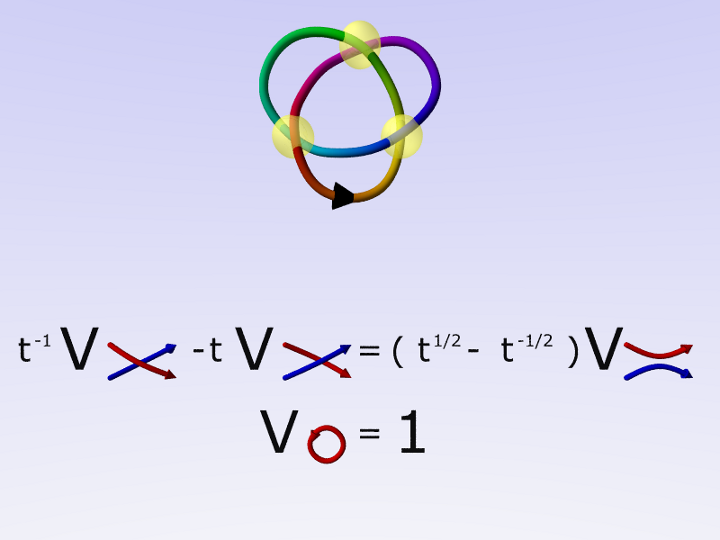
Un modo per calcolare il polinomio di Jones usa la relazione di skein. Il calcolo può essere fatto direttamente sul nodo, senza passare per le trecce.

Capitolo 4 - Danze di Hilden

La danza intorno al palo di maggio è una tradizione in molti Paesi di cultura germanica. Danze simili vengono eseguite anche in Italia meridionale e in Sud America.

I ballerini danzano attorno al palo tenendo in mano le estremità dei nastri fissati in cima al palo. Ballando, i ballerini intrecciano i nastri in vari modi.

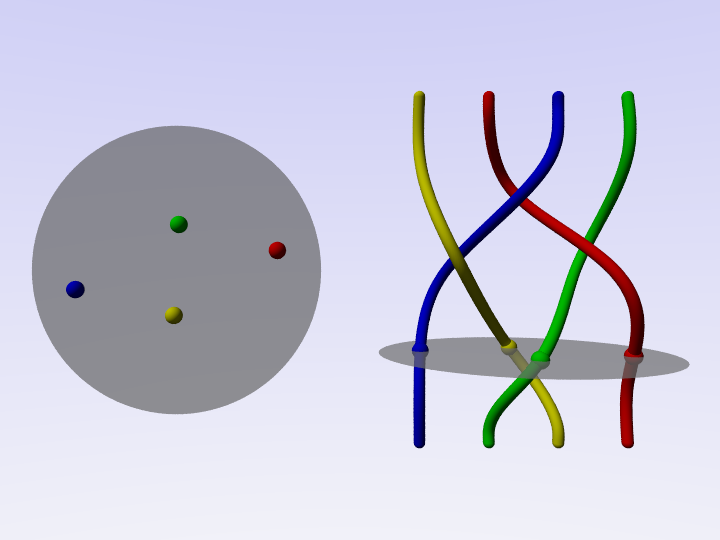
Le danze possono essere formalizzate come movimento di punti nel disco. Tenendo traccia dei movimenti dei punti, si ottiene una treccia.

Viceversa, data una treccia, la si può “rileggere” come una danza.

Consideriamo danze particolari, in cui i ballerini sono a coppie e si tengono per mano. Formalizzando queste danze si ottiene un sottogruppo dei gruppi treccia con un numero pari di fili. Esso viene chiamato gruppo di Hilden.

Un insieme di generatori è dato da tre tipi di treccia, in cui i fili sono condiderati a coppie.

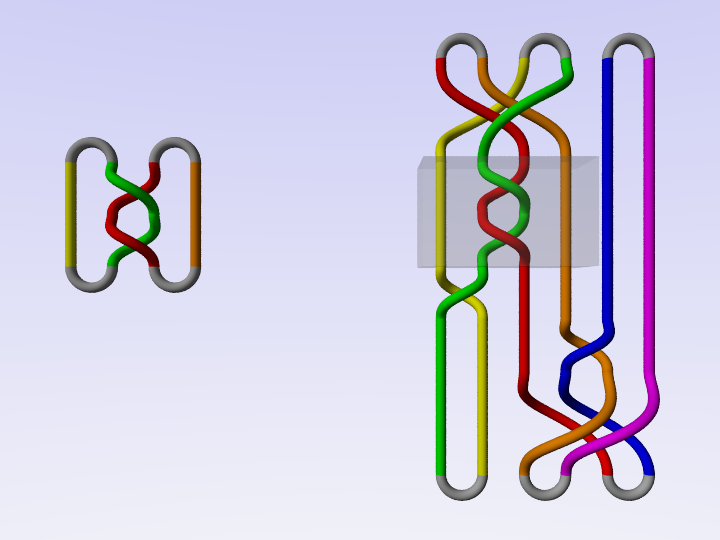
Un altro modo per ottenere dei nodi a partire dalle trecce è la chiusura piatta.

Analogamente a quanto accade per la chiusura di Alexander, ogni nodo può essere ottenuto dalla chiusura piatta di una treccia.

Un teorema di Birman (anni '70 del secolo scorso) caratterizza le trecce che danno lo stesso nodo tramite la chiusura piatta. In altre parole, questo teorema ricalca quello di Markov, ma con una diversa chiusura delle trecce.

Le possibili mosse sono ancora di due tipi: stabilizzazione e composizione con elementi di Hilden.

Infine si enuncia il problema di appartenenza: come è possibile capire se una data treccia appartiene al sottogruppo di Hilden?

Una soluzione si trova in una bozza di articolo del 2009. Non la menzioniamo nel film, ma ci limitiamo a notare che abbiamo trovato un nuovo problema algoritmico, simile a quello trattato nel capitolo 2.